Le billard a été étudié en détail d'un point de vue mécanique par Coriolis il y a 170 ans et plus récemment par Petit (cf. bibliographie). Coriolis est célèbre en mécanique pour la force d'inertie qui porte son nom (la mécanique est une branche de la physique, elle ne nécessite pas de clé de 12). L'étude des statistiques du billard carambole (ou billard français) en revanche est très pauvre. Fray et moi-même avons étudié l'effet de la distance des parties et Shepard (pp. 63–106) a étudié certains aspects statistiques du pool américain. Mais le replacement —bien que central dans les jeux de séries— n'avait pas été étudié.
Jacques Bernoulli est né en Suisse en 1654. Il a posé les bases du calcul des probabilités dans son œuvre majeure (posthume), Ars conjectandi (l'art des conjectures). On dit qu'on a un processus de Bernoulli quand il existe deux états possibles et que chacun a une certaine probabilité constante d'être réalisé. Tirer à pile ou face par exemple est un processus de Bernoulli où chaque résultat possible (pile et face) a une probabilité de 50 %. Jeter un dé n'est pas un processus de Bernoulli parce qu'il existe six résultats possibles. En revanche « obtenir 1 sur un dé » est un processus de Bernoulli parce qu'il n'y a que deux résultats possibles : obtenir 1 (probabilité = 1/6) et ne pas obtenir 1 (probabilité = 5/6).
Considérons le cas suivant. Je jette un dé. Si j'obtiens 1 je perds. Sinon je marque un point et relance le dé. Si j'obtiens 1 je perds. Sinon je marque un autre point et relance à nouveau le dé. Et ainsi de suite jusqu'à obtenir un 1. La probabilité de réussir au moins une fois est 5/6. La probabilité de réussir au moins deux fois est (5/6)2 : il faut réussir la première fois (cinq chances sur six) puis la deuxième fois (cinq chances sur six). Combien de points marquerai-je en moyenne? Le premier lancer me rapporte en moyenne 5/6 point, le deuxième (5/6)2 point, etc. La moyenne est donc 5/6 + (5/6)2 + (5/6)3 + … = 5 points. Plus généralement le score moyen est p / (1 − p) si p est la probabilité de marquer un point. Par exemple à pile ou face, p = 1/2, combien de fois d'affilé devinerai-je juste ? En moyenne 1/2 / (1 − 1/2) = 1 fois.
Le billard français est similaire : si étant donné mon niveau j'ai cinq chances sur six de marquer le point j'aurai une moyenne de 5. Cependant au dé les résultats sont indépendants les uns des autres (ce n'est pas parce que j'ai obtenu un 6 que le lancer suivant aura plus ou moins de chances d'être un 6) alors qu'au billard il existe une corrélation entre les coups : si j'ai un coup facile je peux sans doute rassembler les billes pour avoir un autre coup facile. Même si en moyenne je marque cinq fois sur six, en pleine américaine la probabilité de marquer est beaucoup plus élevée. On n'a donc pas un processus de Bernoulli. Pour connaître ma probabilité de marquer il faut savoir si j'ai ou non l'américaine. Si je réussis le point actuel, aurai-je l'américaine pour le point suivant ? Il faut donc savoir non seulement quelle est ma probabilité de marquer mais aussi quel type de coup j'aurai ensuite. Le processus de Bernoulli est trop simpliste pour tenir compte de tous ces détails. Le suisse ne peut faire face à l'américaine.
La figure ci-dessous représente des résultats de Bernard Villiers au cadre 47/2 (69 reprises). Le modèle bernoullien (pointillés) donne des résultats très différents des données (losanges.) Il sous-estime l'importance des longues séries parce qu'il ne tient pas compte du replacement et du fait que de très longues séries peuvent être ainsi obtenues. Si certains problèmes statistiques ont été étudiées —Fray et moi-même nous sommes par exemple intéressés à des problèmes liés à la longueur des matches—, l'effet du replacement n'avait jamais été étudié.
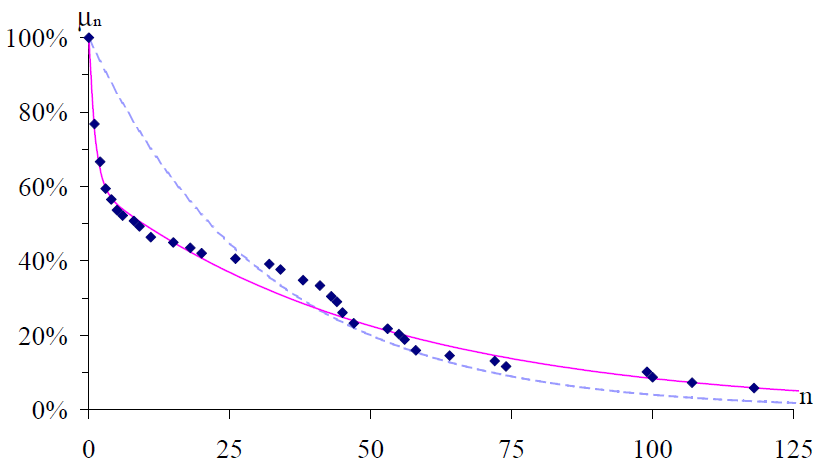
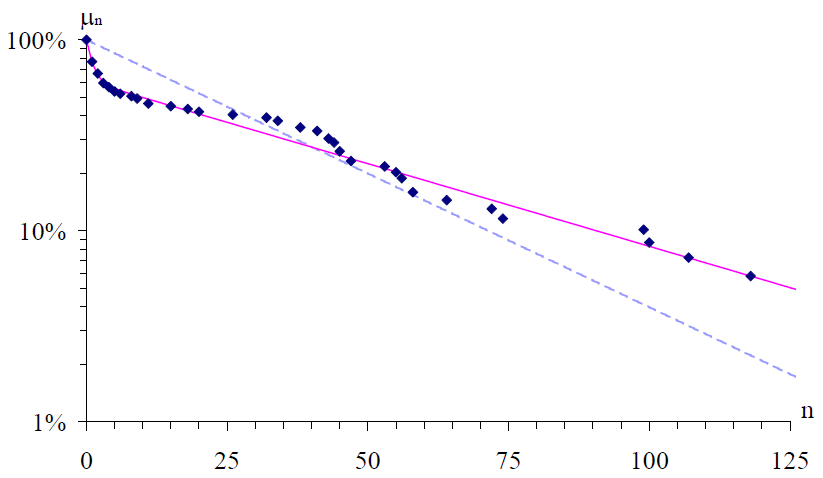
Figure : Probabilité de marquer au moins n points en fonction de n. Gauche : échelle linéaire et droite : échelle semi-logarithmique. Losanges : données de B. Villiers au cadre 47/2 ; ligne pointillée : modèle bernoullien ; ligne continue : modèle markovien.
Andrei Andreyevich Markov est né en Russie en 1856. Il est le célèbre inventeur des chaînes portant son nom. Les chaînes de Markov servent à étudier la succession d'évènements. Prenons l'exemple d'une autre forme de billard, le pool. On considère un match de pool américain où le vainqueur casse. Le fait de casser procure un avantage : le vainqueur de la partie précédente a donc plus de chances de gagner la partie suivante — Shepard (pp. 94–98) considère cette question plus en détail. Supposons que la probabilité de gagner du joueur est de 80 % s'il casse mais de seulement 40 % sinon :
| victoire | défaite | ||
| partie n+1 | victoire | 80 % | 40 % |
| défaite | 20 % | 60 % | |
S'il a une chance sur deux de casser en premier sa probabilité de gagner la première partie est de 80 % × 1/2 + 40 % × 1/2 = 60 %. Pour la partie suivante la probabilité de victoire est 80 % × 60 % + 40 % × 40 % = 64 % et pour celle d'après 80 % × 64 % + 40 % × 36 % = 65,6 %. On aurait pu s'attendre à ce que le joueur gagnant 80 % des parties où il casse et 40 % des autres gagne en moyenne 60 % du temps. En fait plus il gagne plus il a de chances de gagner, donc sa probabilité de gagner une partie est supérieure à 60 %.
Le billard carambole est similaire : un joueur qui a l'américaine a une probabilité très élevée de marquer. On peut ainsi étudier l'occurrence de coups faciles (américaine par exemple) et de coups difficiles. En jouant un coup donné, il y a trois résultats possibles : manquer, marquer en laissant les billes dans une position difficile et marquer en laissant les billes dans une position facile. Si on connaît la probabilité d'obtenir un coup facile après un coup difficile, la probabilité d'obtenir un coup difficile après un coup facile, etc. on peut calculer la probabilité d'avoir une série d'une certaine longueur.
Les lignes continues de la figure ci-dessus représentent la probabilité de marquer au moins n points en fonction de n pour B. Villiers dans le modèle markovien. Les lignes continues sont beaucoup plus proches des résultats de Villiers que les pointillés (Bernoulli). Ceci montre que le modèle markovien est une meilleure description des jeux de séries que le modèle bernoullien.
Il faut noter que, comme toujours dans le domaine des statistiques, il ne s'agit pas de prévoir un évènement précis. Je ne sais pas si cette fois-ci ma pièce va tomber sur pile ou sur face mais je sais qu'en moyenne chaque résultat est obtenu 50 % du temps. Les scores d'un joueur ne nous disent pas quand il a fait une fausse queue ni s'il en fait souvent, mais ils tiennent compte de ce genre d'évènement, vu que tous les coups sont inclus. De même on ne sait pas si tel ou tel coup était facile, mais on peut néanmoins tirer des informations des feuilles de match (il est difficile de donner une explication plus précise sans entrer dans les détails techniques du modèle).
Si après un certain type de coup (facile ou difficile) le joueur a autant de chances d'obtenir un coup facile qu'un coup difficile, il ne joue pas le replacement. S'il a plus de chances d'obtenir un coup facile qu'un coup difficile c'est qu'il joue le replacement. Pour Bernard Villiers (données sur 69 reprises), la probabilité d'obtenir un coup facile ou difficile après un coup facile ou difficile est :
| difficile | facile | |
| difficile | 40,9 % | 1,2 % |
| facile | 11,5 % | 97,8 % |
| manque | 47,6 % | 1,0 % |
Sa probabilité de marquer sur un coup facile est d'environ 99 %. De plus quand il a un coup facile à jouer, grâce au replacement il obtient un autre coup facile près de 98 % du temps mais après un coup difficile il ne parvient généralement pas à obtenir un coup facile. Sa probabilité de marquer sur un coup difficile est à peine supérieure à 50 %.
Les joueurs peuvent calculer ci-dessous leur probabilité d'obtenir un coup facile/difficile après un coup facile/difficile à partir de leurs scores.
| 0 | 5 |
| 1 | 3 |
| 3 | 1 |
| coup difficile n + 1 | probabilité d'obtenir un coup difficile après un coup difficile | probabilité d'obtenir un coup difficile après un coup facile |
| coup facile n + 1 | probabilité d'obtenir un coup facile après un coup difficile | probabilité d'obtenir un coup facile après un coup facile |
Le programme s'occupe des deux dernières étapes si l'utilisateur fournit les données. Si on utilise les résultats de Villiers (fournis) on obtient le tableau ci-dessus.