Everyone knows (and tells children) that, thanks to compound interest, money invested on a savings account will make money if one keeps it there long enough. It is not after a year or two that the interest is of interest, it is when you are really patient. Indeed, did Albert Einstein not call compound interest "the eighth wonder of the world"?
If you invest €10 000 on a savings account at 2%, you get €200 of interest in one year. If you withdraw this interest, then the next year there will be €10 000 on the account, which will again yield €200. In ten years, you will get 10 × €200 = €2 000 worth of interest. This is simple interest.
But if interest is left on the savings account, it will in turn produce interest. The second year there will be €10 200 on the account, which will yield €204 of interest. The third year, €10 404 on the savings account will earn €208 of interest. And so on: instead of gaining every year the same amount, interest will increase steadily over time. The total gain in ten years thus is not 10 × €200 = €2 000, but €2 200. The reason is that the interest is added to the capital, so that interest is paid on capital but also on the interest of the previous years. The interest thus in turn produces interest: it is compound interest.
Except that €2 200 with compound interest instead of €2 000 of simple interest is only 10% more. Simple interest yielded €2 000, and the compounding of interest merely added an extra €200. Apparently the miracle of compound interest is not so miraculous after all. Money invested for ten years at 2% does earn more than 20%, but not much more.
Perhaps you were not patient enough. If you had waited for twenty years, you would have reached a total of €4 860 of interest, or 20% more than simple interest (20 × €200 = €4 000). It is better, but still not miraculous. The compounding of interest has yielded €860: the icing is thicker, but it is still only the icing on the cake.
Here is a little trick to quickly compute compounding. The number of years required to double your capital is (about) equal to 72% divided by the annual rate. It takes for example 72% / 2% ≈ 35 years at 2%, but only 72/3.5 ≈ 20 years to 3.5%. At 3.5%, your capital doubles every twenty years, rising from €10 000 to €20 000 the first twenty years, and again doubling (from €20 000 to €40 000) the next twenty years, and so is worth a little less than €40 000 in 35 years, against only €20 000 at 2%.
The 72% rule is nice to compute things in your head. But another way of using it is to say that what matters is return × time. It takes about 10 years to double your money at 7% but seven decades at 1%. And you can notice that 10 × 7% = 70 × 1%. Investments with the same product of length × annual return will all yield as much. It would be naïve to believe that it takes 50 years at 2% p.a. to double your money (it would ignore compounding). But, as it happens, the product of time and rate makes it nonetheless possible to directly compare investments.
Clearly, the interest rates of savings accounts and bonds fail to really make money, even with compounding. Since the term "interest" applies only to them, I will use the more general term "return", knowing that the annual return of a savings account or a bond is simply the interest rate.
One tells children time and time again that they must be patient and must be prepared to wait before spending their money. This way, compound interest will bring more. Well... no. Compounding really only has value if you wait a long time (not just a few years) and if the annual return is high. Few investors grasp that this latter point is crucial — a low yield for a long time is not a miracle, it is just a waste of time.
If you invest €10 000 at 7% for twenty years, it will reach nearly €29 000 (you will therefore have a total of €39 000). In this case the compounding of returns earned nearly €15 000, slightly more than the simple return (20 × €700 = €14 000). The compounding of returns is not the icing on the cake as with savings accounts and bonds, but downright a second cake.
While the simple return is proportional to the annual return, this is not the case with compounding. In the long run, gains on gains (e.g. interest on interest) can even bring much more than gains on the initial capital if the annual return is high enough and the investment long enough.
The figure below shows that a return apparently three times as high yields more than three times as much. First because, if inflation is at 2.5%, a return of 3% is only a 0.5% gain of purchasing power, i.e. 13 times less than a 9% investment (6.5% real). Moreover, with the compounding of returns over the long term (30 years here), interest on interest (or gains on gains, orange) yield significantly more that the gains on the initial capital (blue) if the real return is high enough. Thus, a 9% return gains 35 times as much in 30 years as a 3% investment. Now, it is the simple return on capital (in blue) which is the icing on the cake!
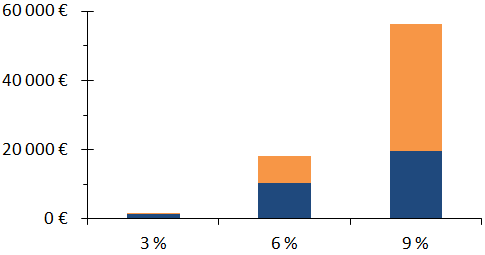
Figure: Real gains on €10 000 invested for 30 years at various nominal returns (inflation of 2.5%). The simple returns are in blue, and the orange part gives the contribution of compounding.
It is only if you have time and if the real return is high that compounding works wonders. So compound interest can never bring in a lot because the interest (be it from savings accounts or bonds) is never much above inflation and therefore does not fulfill the second condition. Compound interest is not a wonder, but compound returns can be really wonderful indeed.