Imagine that your child asks who will win in a game of the goose (or snakes and ladders) well under way. How could you tell? By doing a Monte Carlo simulation.
We ask a computer to choose a random number from 1 to 6, we move by this number of spaces and we apply the rules of the space on which we land. Then we do the same with the next player, and so on until someone wins.
Except that it is obvious that with different die results the winner could have been different. So we start all over again: we ask a computer to choose a new random number between 1 and 6, we move by this number of spaces, we apply the rule of the space on which we land, then we do the same with the next player. And again, and again, and again. We simulate a thousand games. We simulate a million games. And we conclude that the red player wins 42.6% of the time, blue 32.8% and yellow 24.6%. (This does not tell us who will win the current game, but it does give us the probability of each player winning.)
The basic principle of a Monte Carlo simulation is no more complicated than this.
The outcome of a random phenomenon cannot be predicted (for example roulette). A random number is a number picked at random (e.g. by rolling a die).
When a computer is asked for a random number, what it generates is in fact a pseudo-random number. The sequence of numbers produced appears random (there seems to be no link between successive numbers) but this is not really the case. (In practice we often refer to them simply as random numbers, but bearing in mind that they are not.)
A probabilistic (a.k.a. stochastic) simulation is a numerical simulation based on random numbers. The result will be in the form of a probability, whereas with deterministic simulations, the outcome is always the same.
In some cases you know perfectly well what will happen: when I hit a tennis ball with a racket, I know where the ball will go. Its trajectory is not due to chance: it is entirely determined by the initial position of the ball, the force, the orientation of the racket, etc. — the trajectory is deterministic. Lotteries, by contrast, are matters of chance. But there are more subtle situations, at the boundary between deterministic and non-deterministic.
The weather for example is not due to chance (it obeys the laws of physics) but it is nonetheless hard to forecast. A situation that is both deterministic in theory and hard to predict in practice is said to be chaotic.
Throwing a coin or die is chaotic enough for the result to be considered random. But in some cases the deterministic aspect comes back with a vengeance: it is possible to cheat at roulette with a camera locating the moving ball in relation to the numbers and a computer calculating which numbers it will probably stop on.
Conversely, it is sometimes possible to treat in a non-deterministic way a phenomenon which is in fact deterministic. For example, the weather two weeks from now is not really random, but it would be hard to know in advance. We can therefore use statistics saying that at this time of year the probability of rainfall is 15% and in the simulation use random numbers to decide whether it will rain.
Monte Carlo simulations are therefore not useful only in truly random situations (such as the game of the goose). They can also be used when deterministic details give seemingly random results. There is therefore a decision to be made in modeling: will we treat the phenomenon of interest as deterministic or not? Thus, in science, we can sometimes calculate precisely what can happen, but at other times (including for the same phenomenon) we merely say that this or that event has a certain probability of happening and we look at the consequences.
In addition to the obvious application of gambling, let's look at the use of Monte Carlo simulations for two applications: physics and for investments.
We want to study the movements (the so-called diffusion) of an atom, for example on a surface. We say that, in a nanosecond (1 ns), the atom has a certain probability of moving to the left, to the right, up or down. It may also not move. The sum of these five probabilities is of course 100%. The probabilities of the four directions may be identical (isotropy) or there may be up to four different values.
A random number is thus drawn to decide where the atom goes. (It's like throwing a five-sided die, but each side could have a different size.) The operation is repeated for the next nanosecond, and the next, and so on. It is thus possible to create image by image the film of the movements of this atom.
Obviously, with different random numbers we would have obtained a different result. So we start over to get a new trajectory, and another, and another. A few thousand or million trajectories later, we have statistics: we can know for example the average distance traveled from the starting point, the direction, etc.
The diffusion of an atom is not really entirely due to chance, it is just that the phenomenon is so complicated (chaotic) that the issue seems random. We can also simulate diffusion with deterministic techniques, such as molecular dynamics. The advantage of Monte Carlo is that we do not deal with all the details that take time to calculate and focus instead on their consequences (the probabilities of the different events): the simulation therefore runs much faster. On the other hand, it requires to simplify (and therefore to ignore certain details) and data on probabilities (coming from experiments or deterministic simulations).
With investments like stocks, we do not know in advance how much we will get out. We know that in the long term stocks gain more than bonds, but we do not know if the stock market will go up or down tomorrow. We can therefore simulate markets as a series of die rolls: as with dice, we do not know the results one by one, but we do know their average (the average yield of the stock market). So Monte Carlo simulations can be very useful for financial planning.
Imagine that you are in the following situation:
Each year, the difference between income and expenses is invested in a stock–bond portfolio. For how long can you afford to withdraw money from your savings?
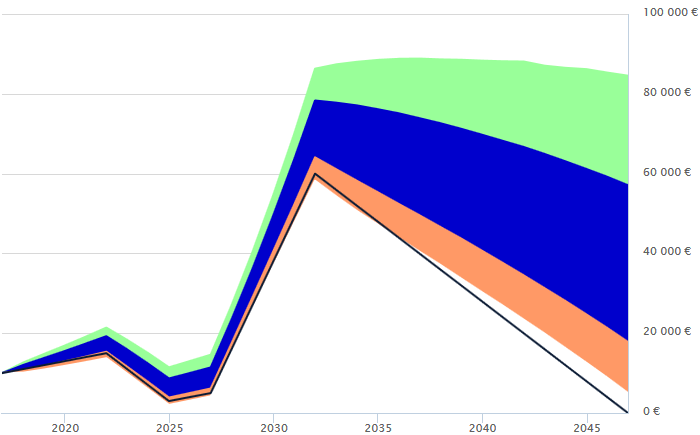
You do not have a clue, I suppose. And yet one can answer the question: with a Monte Carlo simulation. That is to say, we simulate thousands of possible evolutions of the markets and look at how long you last on average, or how likely you are to be broke in thirty years, etc.
Since the market performance is not known in advance, the result is a range of possibilities: most of the results (60%) will be in the blue zone, with orange and green areas representing 15% of the probabilities each. There is a probability of 5% above the green and as much below the orange. The black line in the figure corresponds to cumulative savings (i.e. excluding profits and losses on investments).
The result of the simulation above shows two bottlenecks, in 2025 and 2047. This information allows you to plan your finances to reduce your expenses a few years earlier and then simulate again until you get a satisfactory result — that is, until your strategy gives you a good probability of achieving all your goals.
We could go further and combine Monte Carlo simulations with a program optimizing asset allocation over time to maximize your probability of achieving your goals, for more advanced financial planning. (The stock allocation, for instance, would be higher in the accumulation phase and lower in retirement.)