Would you rather have to save €25 000 or €85 000 to prepare for retirement?
Everyone would rather choose €25 000. Yet, many people will need to save €85 000.
If you are preparing for retirement and have thirty years ahead of you, a €10 000 investment will earn you less than €2 000 on a savings account but more than €30 000 on average in stocks. If you want to have €100 000 in thirty years (that is to say have the purchasing power of €100 000 of today's money), you must save €85 000 in a savings account or less than €25 000 on average in the stock market.
In the first case your gains correspond to a fraction of the capital invested, while in the second case it is three times the capital you originally invested. This is no longer the icing on the cake, it means three extra cakes.
The figure below clearly shows that with an investment earning much more than inflation, the capital required today to have €100 000 in thirty years is not exorbitant. Gains on investment do the rest.
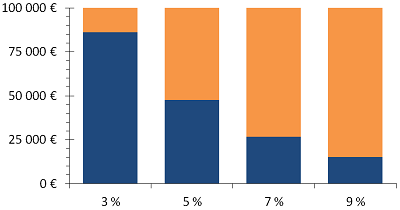
Figure: Capital needed to have €100 000 in thirty years (inflation of 2.5%). Savings are in blue and gains in orange.
There are two schools of thought: there are those who save a lot of money (the blue bars are then the main contributors toward the €100 000 available thirty years later) and there are those who invest their money efficiently (and therefore need far less money initially). The figure above shows that €85 000 merely set aside on a savings account (instead of being invested) thirty years before retirement do not necessarily provide you with a better retirement than €25 000 well invested. Starting early to prepare for retirement is good, doing it effectively is better.
One too often tends to compare interest rates as if a 4% rate were to bring in twice as much as 2%. But if you take into account both inflation and the compounding of returns, you will see that an investment of 9% per year gained 35 times more purchasing power in thirty years than a 3% investment (with 2.5% of inflation), rather than 3 times as might be expected.
If you do not account for compounding and inflation, it seems that the gain is 2.5 times higher (7.5% against 3%) and not 20 times. If you do not grasp the crucial influence of inflation and compounding, you cannot understand why investing your money well is at least as important as saving.
You will reply that savings accounts or bonds that pay 9% p.a. do not exist. And you will be right. But in the long term stock investments gained on average 6–6.5% per year above inflation (but before fees and taxes). And anyway, there is no need to get exactly this return: if you get a return 5% above inflation, you already earn 20 times as much in thirty years as with an investment yielding only 0.5% above inflation.
